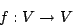- ... multiplizieren1.1
- Bemerke, in der Matrix
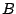 habe ich
habe ich 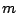 und
und 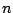 vertauscht, da man eine
vertauscht, da man eine 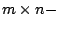 Matrix nur mit einer
Matrix nur mit einer 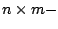 Matrix multiplizieren kann.
Matrix multiplizieren kann.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Matrizen1.2
- In quadratischen Matrizen stimmt die Zeilenanzahl mit der Spaltenanzahl überein.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... haben1.3
- Also gibt es unterhalb der Diagonalen nur Nullen. Eine solche Matrix nennt man Dreiecksmatrix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... erste2.1
- natürlich auch die anderen beiden
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Addition2.2
- Da
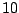 keine Primzahl ist, ist die Restklasse
keine Primzahl ist, ist die Restklasse 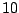 kein Körper.
kein Körper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Faktoren2.3
- In der Schule heißt dieses Verfahren Primfaktorzerlegung.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Tupel3.1
- Aus Platzgründen schreiben wir hier das Tupel horizontal statt vertikal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Basis3.2
- Siehe Definition Basis
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
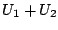 3.3
3.3
- Die Summe der beiden Vektorräume ist definiert durch
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dann4.1
- Die Betragsstriche bedeuten hierbei die Mächtigkeit von X. D.h. die Anzahl der Elemente in X.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gilt4.2
- Dies kann man beweisen, indem man die einzelnen Polynome explizit hinschreibt. Dann kann man hingehen und sie umformen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Isomorphismus4.3
- also injektiv
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... soll6.1
- Den Satz kann man auch für
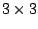 Matrizen anwenden.
Matrizen anwenden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... können6.2
- Das geht beim Endomorphismus, da er ja eine Abbildung in demselben Vektorraum ist
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nämlich7.1
- Beweis dazu auf S. 211 des Buches
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
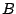 habe ich
habe ich 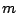 und
und 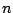 vertauscht, da man eine
vertauscht, da man eine 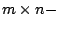 Matrix nur mit einer
Matrix nur mit einer 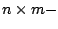 Matrix multiplizieren kann.
Matrix multiplizieren kann.
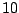 keine Primzahl ist, ist die Restklasse
keine Primzahl ist, ist die Restklasse 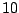 kein Körper.
kein Körper.
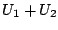 3.3
3.3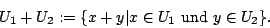
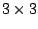 Matrizen anwenden.
Matrizen anwenden.