X → X ::: Lineare Algebra

Menü

Informatik » Bachelor » Lineare Algebra » Abbildungen, insbesondere lineare » Beweise für injektiv, surjektiv und bijektiv » X → X

Beweise für injektiv, surjektiv und bijektiv Beweise für injektiv, surjektiv und bijektiv F injektiv ⇔ Ker (F) = 0

X → X

Sei $f:X\rightarrow X$ . Folgende Aussagen sind äquivalent:
(i)

ist injektiv
(ii)

ist surjektiv
(iii)

ist bijektiv

(iii) $\rightarrow$ (i) oder (ii) $\,\,\,\,$ und $\,\,\,\,$ (i) und (ii) $\rightarrow$ (iii) $\,\,\,\,$ sind klar.
Zu beweisen ist 1. (i) $\rightarrow$ (ii) und 2. (ii) $\rightarrow$ (i)

injektiv 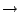$\rightarrow$ surjektiv. Wir beweisen dies, indem wir zeigen, daß ,,nicht surjektiv 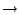$\rightarrow$ nicht injektiv''. Mit anderen Worten: Die Abbildung ist surjektiv, wenn sie injetktiv ist, da sie, wenn sie nicht surjektiv wäre, auch nicht injektiv sein könnte:
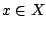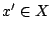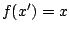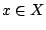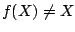Surjektiv bedeutet, daß es für alls $x\in X$ in der Zielmenge ein $x'\in x$ in der Ausgangsmenge gibt, so daß gilt . Ist eine Abbildung nicht surjektiv, so hat ein $x\in X$ in der Zielmenge kein Urbild. Es gilt also $f(X)\not= X$ .
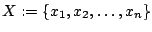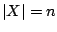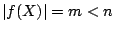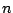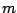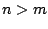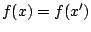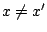Sei $X:=\{x_{1},x_{2},\ldots,x_{n}\}$ also $\vert X\vert=n$ , dann^4.1 ist $\vert f(X)\vert=m<n$ . Nun sagt das Schubfachprinzip von Dirichlet, daß, wenn wir Objekte in Schubladen legen, wobei , in einer Schublade in allen Fällen mehr als ein Objekt liegen muß. Folglich ist die Injektivität nicht gegeben, da aber $x\not=x'$ (nämlich genau in dem Schubfach, wo zwei Objekte liegen.)
$\Box$
surjektiv 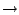$\rightarrow$ injektiv. Wir beweisen, daß wenn die Abbildung nicht injektiv ist, sie auch nicht surjektiv ist.
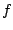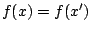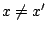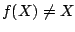Ist nicht injektiv, so gibt es mit $x\not=x'$ . So ist $f(X)\not=X$ und da mindestens ein Element in 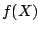fehlt mindestens 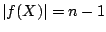$\vert f(X)\vert=n-1$ , so daß 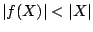$\vert f(X)\vert<\vert X\vert$ und somit die Abbildung nicht surjektiv ist, da es 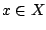$x\in X$ in der Zielmenge gibt, für die es kein 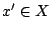$x'\in x$ in der Ausgangsmenge gibt.

Beweise für injektiv, surjektiv und bijektiv Beweise für injektiv, surjektiv und bijektiv F injektiv ⇔ Ker (F) = 0