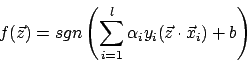Unterabschnitte
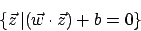
Die eine Halbebene ist dann definiert durch
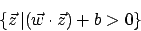
die andere durch
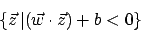
Für viele separierbare Probleme können wir eine Hyperebene auf verschiedene Art und Weise erstellen
![\includegraphics[scale=0.5]{verschiedeneebenen.eps}](img260.png) Wir sehen jedoch, dass viele Ebenen nicht so klug separieren. Wenn wir gerade an einen Rand die Ebene legen, dann können leicht Muster auftauchen, die die Ebene überschreiten. Wir wollen deshalb eine Ebene mit einem Korridor drumherum erstellen
Wir sehen jedoch, dass viele Ebenen nicht so klug separieren. Wenn wir gerade an einen Rand die Ebene legen, dann können leicht Muster auftauchen, die die Ebene überschreiten. Wir wollen deshalb eine Ebene mit einem Korridor drumherum erstellen
![\includegraphics[scale=0.5]{korridor.eps}](img261.png) Wir können
Wir können 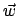 und
und 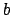 so einstellen, dass alle Punkte außerhalb des Korridors liegen und die Support Vectors genau auf der Grenze:
so einstellen, dass alle Punkte außerhalb des Korridors liegen und die Support Vectors genau auf der Grenze:
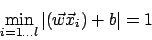
Seien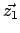 und
und 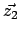 die Support Vectors, dann gilt
die Support Vectors, dann gilt
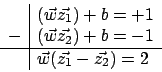
Wir normieren
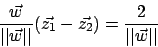
und erhalten ein passendes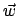
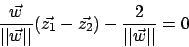
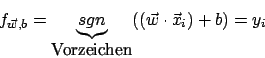
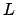 hat die Form
hat die Form
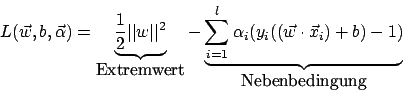
Nach Einsetzen und Auflösen erhalten wir die sogenannte Duale Form
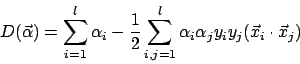
Die Decision Function wäre dann
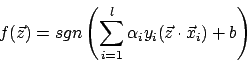
Linear separierbare Probleme
Linear separierende Ebene mit Korridor
Wir können einen Vektorraum durch eine Hyperebene eine Dimension tiefer in zwei Teile teilen. Linear sparierbare Probleme lassen sich durch eine Hyperebene in zwei Klassen teilen. Eine solche Hyperebene läßt sich definieren durchDie eine Halbebene ist dann definiert durch
die andere durch
Für viele separierbare Probleme können wir eine Hyperebene auf verschiedene Art und Weise erstellen
![\includegraphics[scale=0.5]{verschiedeneebenen.eps}](img260.png)
![\includegraphics[scale=0.5]{korridor.eps}](img261.png)
Seien
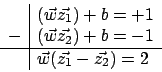
Wir normieren
und erhalten ein passendes
Decision Function
Unsere Entscheidungsfunktion ist nun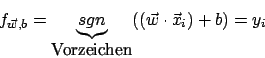
La Grange
Wir versuchen zwei Ziele zu erfüllen- gute Generalisierung (Extremum)
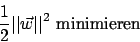
- alle Beispiele richtig klassifizieren (Nebenbedingung)
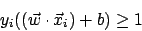
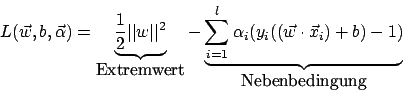
Nach Einsetzen und Auflösen erhalten wir die sogenannte Duale Form
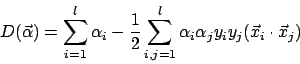
Die Decision Function wäre dann