Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Der Vektorraum » Austauschsatz von Steinnitz » Formulierung Austauschsatz von Steinnitz
Austauschsatz von Steinnitz Austauschsatz von Steinnitz Beweis des Austauschsatzes von Steinnitz

Formulierung Austauschsatz von Steinnitz

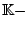
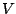
In einem $\mathbb{K}-$Vektorraum $V$ seinen eine Basis

\begin{displaymath}B:=\{v_{1},\ldots,v_{r}\}\end{displaymath}

und eine linear unabhängige Familie

\begin{displaymath}(w_{1},\ldots,w_{n})\end{displaymath}

gegeben.
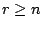
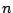
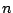
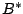
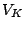
Es ist $r\geq n$. Man kann $n$ Vektoren der Basis durch die $n$ Vektoren der linear unabhängigen Familie ersetzen, so daß die neue Basis $B^{\ast}$ wieder linear unabhängig ist und eine Basis des Vektorraums $V_{K}$ ist. Nach eventueller Umnummerierung der Indizes kann man so schreiben:

\begin{displaymath}B^{\ast}:=\{w_{1},\ldots,w_{n},v_{n+1},\ldots,v_{r}\}\end{displaymath}

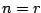
oder im Spezialfall $n=r$:

\begin{displaymath}B^{\ast}:=\{w_{1},\ldots,w_{n}\}\end{displaymath}


Austauschsatz von Steinnitz Austauschsatz von Steinnitz Beweis des Austauschsatzes von Steinnitz