Unterabschnitte
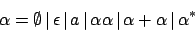
Syntaxdiagramm:
Beispiele für Syntaxdiagramme sehen wir gleich noch.
Regulärer Ausdruck
Zu jedem regulären Ausdruck 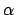 gibt es einen NFA
gibt es einen NFA 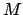 , so daß gilt
, so daß gilt
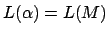
1.Verfahren:
Zu einem regulären Ausdruck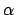 gehört eine Sprache
gehört eine Sprache 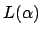 die wie folgt definiert ist:
die wie folgt definiert ist:
Dies läßt uns erkennen, wie wir einen Automaten aus einem regulären Ausdruck bilden können. Wir können dies, indem wir triviale Automaten für Teilausdrücke zur Verfügung stellen und mit diesen Operationen für die Vereinigung, den Durchschnitt und den Kleenabschluß durchführen:
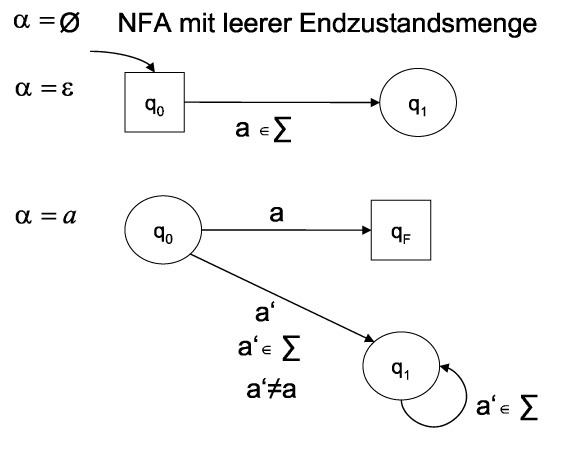
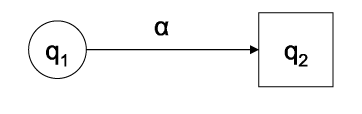 Wenn
Wenn
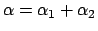 :
:
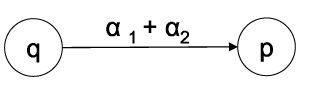

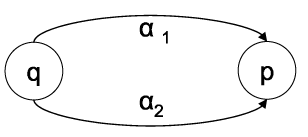 Wenn
Wenn
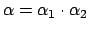 :
:
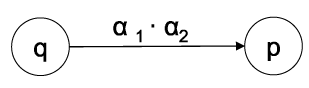

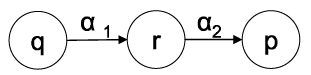 Wenn
Wenn
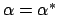 :
:
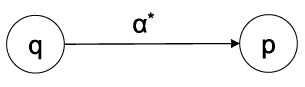

DFA
Zu jedem DFA 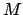 gibt es einen regulären Ausdruck
gibt es einen regulären Ausdruck 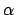 , so daß gilt
, so daß gilt
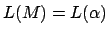
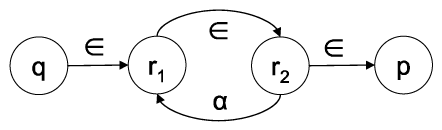
Wir wenden das Verfahren des dynamischen Programmierens an. Dabei erstellen wir für Teilmengen an Zuständen des DFAs reguläre Ausdrücke und fügen diese zu immer größer werdenden Teilmengen zusammen. Wir starten dabei bei Teilmengen aus zwei oder einem Zustand, wobei bei zwei Zuständen diese Zustände direkt verbunden sein müssen.
Es gilt für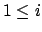 und
und 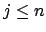 :
:
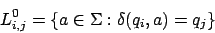
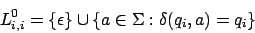
Wir können folgende reguläre Ausdrücke erzeugen:
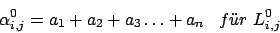
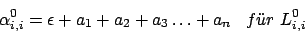
Diese Ausdrücke können wir nach folgender Formel zusammenfügen
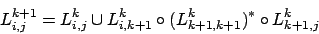
Wieder der reguläre Ausdruck
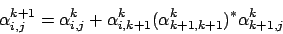
Reguläre Ausdrücke
Syntax regulärer Ausdrücke
Induktive Definition: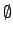 und
und 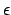 sind reguläre Ausdrücke
sind reguläre Ausdrücke
- für jedes
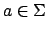 ist
ist 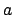 ein regulärer Ausdruck (alle Zeichen sind in sich selbst ein regulärer Ausdruck)
ein regulärer Ausdruck (alle Zeichen sind in sich selbst ein regulärer Ausdruck)
- Mit
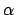 und
und 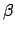 sind auch
sind auch 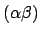 ,
,
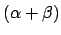 und
und 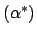 reguläre Ausdrücke.
reguläre Ausdrücke.
- Nichts sonst ist ein regulärer Ausdruck
Syntaxdiagramm:
Beispiele für Syntaxdiagramme sehen wir gleich noch.
Regulärer Ausdruck 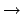 NFA
NFA
Zu jedem regulären Ausdruck 1.Verfahren:
Zu einem regulären Ausdruck
|
|
|
|
|
|
|
|
|

2.Verfahren:
Wir können aus einem initialen NFA einen äquivalenten NFA zum regulären Ausdruck konstruieren, indem wir die Kanten rekursiv ersetzen:
Initialer NFA:

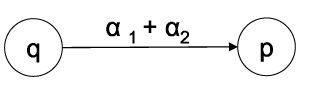


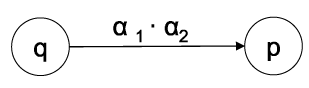





DFA 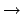 regulärer Ausdruck
regulärer Ausdruck
Zu jedem DFA Wir wenden das Verfahren des dynamischen Programmierens an. Dabei erstellen wir für Teilmengen an Zuständen des DFAs reguläre Ausdrücke und fügen diese zu immer größer werdenden Teilmengen zusammen. Wir starten dabei bei Teilmengen aus zwei oder einem Zustand, wobei bei zwei Zuständen diese Zustände direkt verbunden sein müssen.
Es gilt für
Wir können folgende reguläre Ausdrücke erzeugen:
Diese Ausdrücke können wir nach folgender Formel zusammenfügen
Wieder der reguläre Ausdruck