Unterabschnitte
DFA
Wir können aus einem DFA eine reguläre Grammatik machen.
Dazu verwenden wir folgende Regeln:
NFA
Beim Überführen von einem NFA in einen DFA generieren wir die Potenzmenge der Zustände des NFAs. D.h. das wir aus allen Untermengen der Menge 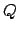 einen neuen Zustand machen.
einen neuen Zustand machen.
Wir generieren den neuen DFA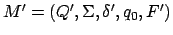 wie folgt:
wie folgt:
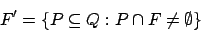
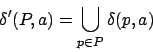
Da dies niemand verstehen kann, hier noch einmal eine Konstruktionsvorschrift für den DFA. Zur Konstruktion müssen wir folgendes tun:
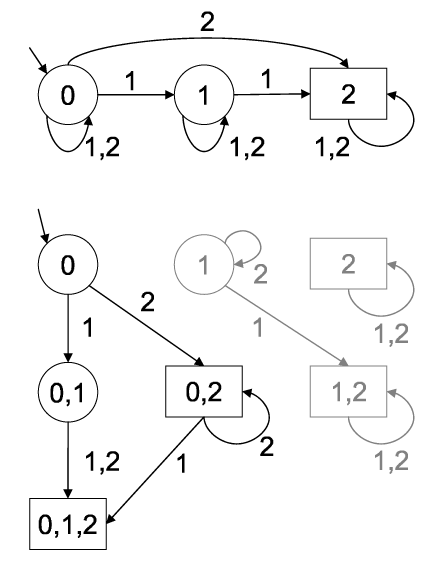 Die grauen Knoten und Kanten kann man auch weglassen, da sie nie erreicht werden. Formal werden sie aber auch bei der Konstruktion erzeugt.
Die grauen Knoten und Kanten kann man auch weglassen, da sie nie erreicht werden. Formal werden sie aber auch bei der Konstruktion erzeugt.
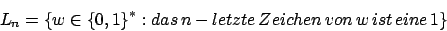
Reguläre Grammatik
Wir können aus einer regulären Grammatik einen NFA machen:
- Übersicht
- DFA
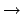 reguläre Grammatik
reguläre Grammatik
- NFA
 DFA (Potenzmengenkonstruktion)
DFA (Potenzmengenkonstruktion)
- Effizienz von NFAs
- Reguläre Grammatik
 NFA
NFA
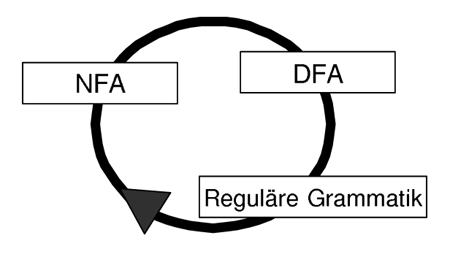
Endliche Automaten und reguläre Grammatiken
Übersicht

DFA  reguläre Grammatik
reguläre Grammatik
Wir können aus einem DFA eine reguläre Grammatik machen.
Dazu verwenden wir folgende Regeln:
| Wenn |
|
| Wenn |
|
| Wenn |
|
NFA  DFA (Potenzmengenkonstruktion)
DFA (Potenzmengenkonstruktion)
Beim Überführen von einem NFA in einen DFA generieren wir die Potenzmenge der Zustände des NFAs. D.h. das wir aus allen Untermengen der Menge Wir generieren den neuen DFA
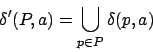
Da dies niemand verstehen kann, hier noch einmal eine Konstruktionsvorschrift für den DFA. Zur Konstruktion müssen wir folgendes tun:
- Potenzmenge der Zustände des NFAs bilden und alle Zustände aufmalen. Dabei darauf achten, daß die Potenzzustände, in denen ein Endzustand vorkommt auch Endzustände werden. (erste Regel)
- Nun die Übergangsfunktionen in Form von Pfeilen mit Inschriften einzeichnen. Dabei betrachten wir für jeden Potenzzustand alle Symbole des Eingabealphabetes. Sei nun das aktuelle Symbol gerade
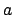 .
.
- Wir legen uns eine Menge
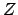 an.
an.
- Nun gehen wir jeden Zustand, der in unserem Potenzzustand vorhanden ist, durch. Können wir von diesem Zustand in dem NFA einen anderen Zustand oder vielleicht sogar mehrere mit Hilfe von
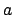 erreichen? Dann kommen diese Zustände in die Menge
erreichen? Dann kommen diese Zustände in die Menge 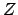 .
.
- Wenn wir alle Zustände im vorhergehenden Schritt abgearbeitet haben, dann haben wir einen Potenzzustand in der Menge
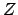 stehen, zu dem wir nun einen Pfeil mit der Inschrift
stehen, zu dem wir nun einen Pfeil mit der Inschrift 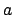 malen.
malen.
- Wir legen uns eine Menge

Effizienz von NFAs
Der DFA zu einem NFA hat im schlechtesten Falle exponentiell viele Zustände wie der NFA. Es gibt Sprachen, die sich durch NFAs viel besser darstellen lassen, wie zum Beispiel
Reguläre Grammatik 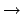 NFA
NFA
Wir können aus einer regulären Grammatik einen NFA machen:
- Jedes Non-Terminal wird zu einem Zustand konvertiert.
- Dazu kommt der Zustand
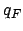 , welcher Endzustand ist.
, welcher Endzustand ist.
- Existiert in der Grammatik eine Regel
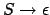 , wobei
, wobei 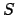 Startzustand ist, so ist im NFA
Startzustand ist, so ist im NFA 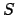 ein Endzustand. Dadurch wird erreicht, daß auch das leere Wort akzeptiert wird.
ein Endzustand. Dadurch wird erreicht, daß auch das leere Wort akzeptiert wird.
- Wenn es eine Regel
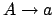 gibt, dann kreiren wir eine Übergangsfunktion
gibt, dann kreiren wir eine Übergangsfunktion 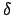 (zeichnen einen Pfeil) von dem Zustand
(zeichnen einen Pfeil) von dem Zustand 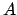 nach
nach 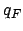 mit der Inschrift
mit der Inschrift 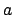 .
.
- Wenn es eine Regel
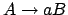 gibt, dann kreiren wir eine Übergangsfunktion (zeichnen einen Pfeil) von dem Zustand
gibt, dann kreiren wir eine Übergangsfunktion (zeichnen einen Pfeil) von dem Zustand 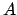 in den Zustand
in den Zustand 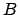 mit der Inschrift
mit der Inschrift 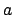 .
.
- Wenn es eine Regel