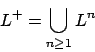Ψ Die Informatikseite

Menü
Informatik » Bachelor » Theoretische Informatik » Allgemeines » Formale Sprachen
Äquivalenzrelation Allgemeines Berechenbarkeit

Formale Sprachen

Eine Sprache besteht aus Wörtern. Hierfür gibt es meistens Regeln, wie Wörter dieser Sprache gebildet werden, manchmal werden die Wörter aber auch explizit angegeben.
leere Sprache $L=\{\}$ oder auch $L=\emptyset$
Länge des Wortes Die Länge des Wortes ist die Anzahl der Symbole, die es aus $\Sigma$ umfaßt.
Leeres Wort $w_{\epsilon}=\epsilon$
Inverses Wort $w^{R}$
Konkatenation: $L=L_{1}\circ L_{1}$ bedeutet ( $w_{1}\in L_{1}$, $w_{2}\in L_{2}$) $w=w_{1}w_{2}$.
Konkatenation läßt sich mehrfach wiederholen. Beispielsweise bedeutet $L^{n}$ n mal L:

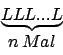
\begin{displaymath}\begin{array}{c} \underbrace{LLL...L}\\ n\, Mal\\ \end {array}\end{displaymath}

Kleenabschluß: Unter dem Kleenabschluß versteht man

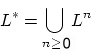
\begin{displaymath}L^{*}=\bigcup_{n\geq 1}L^{n}\end{displaymath}

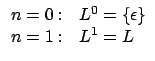
Für $\begin {array}{ll}n=0:&L^{0}=\{\epsilon\}\\ n=1:&L^{1}=L\\ \end {array}$

$L^{+}$ steht für2

\begin{displaymath}L^{+}=\bigcup_{n\ge 1}L^{n} \end{displaymath}


Fußnoten

... für2
Genauso wie $L^{*}$, nur daß die Menge mit dem leeren Wort ausgeschlossen ist.

Äquivalenzrelation Allgemeines Berechenbarkeit