Unterabschnitte
SAT
3SAT ist das Erfüllbarkeitsproblem mit der Voraussetzung, daß in der Formel 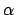 höchstens 3 Literale pro Klausel sein dürfen.
höchstens 3 Literale pro Klausel sein dürfen.
Es ist klar, daß man für den NP-Vollständigkeitsbeweis genauso wie bei SAT die Guess-And-Check-Methode bei 3SAT anwenden kann.
Wir können SAT auf 3SAT polynomiell reduzieren:
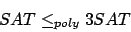
1.Schritt
Mit Hilfe der De-Morgan-Regeln
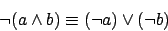
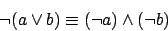
und der Regel der doppelten Verneinung
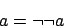
erstellen wir einen Syntaxbaum aus der Eingabeformel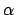 , in dem die Negationen nur in den Blättern vorhanden sind. Der so entstandene Syntaxbaum ist offensichtlich äquivalent zu der Eingabeformel
, in dem die Negationen nur in den Blättern vorhanden sind. Der so entstandene Syntaxbaum ist offensichtlich äquivalent zu der Eingabeformel 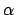 .
.
2.Schritt
Wir formen den so entstandenen Syntaxbaum um.
Dafür geben wir einem jeden Verknüpfungsknoten einen Namen, wobei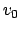 der Wurzelverknüpfungsknoten ist.
der Wurzelverknüpfungsknoten ist.
Nun kommt ein Äquivalenzoperator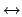 ins Spiel. Wir definieren denselben folgendermaßen35:
ins Spiel. Wir definieren denselben folgendermaßen35:
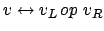 bedeutet:
bedeutet:
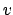 ist 1, wenn
ist 1, wenn
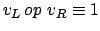
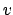 ist 0, wenn
ist 0, wenn
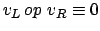
Wir können auch folgendes Konstrukt erstellen:
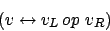
Dies bedeutet, daß wenn der rechte und der linke Teil äquivalent sind, die Formel 1 ist, wenn beide Teile nicht äquivalent sind, dann ist der Wert der Formel 0. Wir können uns dies an einem Beispiel36 klar machen:
Aufgrund dieser Wahrheitstabellen können wir nun die Formeln 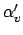 konstruieren:
konstruieren:
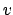 des Syntaxbaumes eine solche Formel
des Syntaxbaumes eine solche Formel 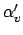 erstellen. Diese fügen wir zusammen:
erstellen. Diese fügen wir zusammen:

In den obigen Formel bemerken wir, daß wir höchstens immer 3 Literale pro Klausel in der Formel stehen haben37. Die Formeln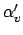 sind also 3KNF Formeln. Somit ist auch
sind also 3KNF Formeln. Somit ist auch 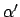 eine 3KNF Formel. Wir können uns klar machen, daß
eine 3KNF Formel. Wir können uns klar machen, daß
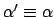 .
.
3SAT
3SAT 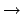 CP:
CP:
Wir erzeugen den Graphen für das CP folgendermaßen: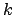 gibt, wobei
gibt, wobei 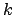 die Anzahl der Klauseln in 3SAT ist, so ist die Formel erfüllbar.
die Anzahl der Klauseln in 3SAT ist, so ist die Formel erfüllbar.
Beispiel
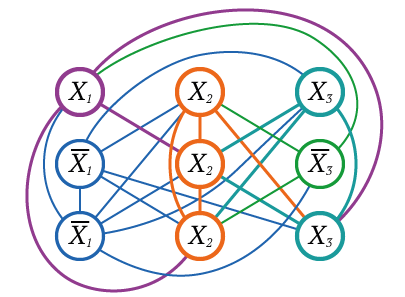 Da es eine Dreier-Clique gibt, ist die aussagelogische Formel für eine Belegung wahr.
Da es eine Dreier-Clique gibt, ist die aussagelogische Formel für eine Belegung wahr.
3SAT
Gliedert sich in 2 Teile:
Für die NP-Vollständigkeit von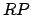 genügt es nachzuweisen, daß
genügt es nachzuweisen, daß
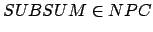 , da
, da 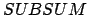 ein Spezialfall von
ein Spezialfall von 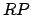 ist. Um
ist. Um 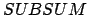 auf
auf 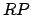 zu reduzieren38 setzen wir das Gewicht für jedes Element gleich 1.
zu reduzieren38 setzen wir das Gewicht für jedes Element gleich 1.
Die Frage von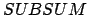 ist es nun:
ist es nun:
Es gilt zu beweisen39:
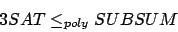
Sei die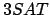 -Formel von der folgenden Form:
-Formel von der folgenden Form:
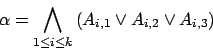
Die i-te Klausel hat folgende Form:
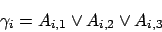
Wir setzen den zu erzielenden Gewinn gleich40
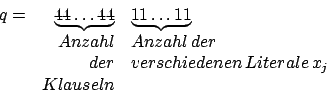
Wir erstellen für jedes Literal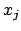 vier Gewinne für
vier Gewinne für 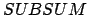 41:
41:
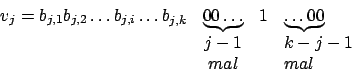
Dabei stellt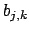 das Vorkommen von
das Vorkommen von 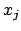 in der k-ten Klausel da.
in der k-ten Klausel da.
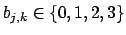
Dasselbe für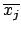 :
:
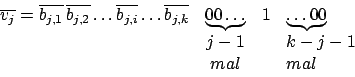
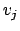 und
und
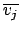 garantieren, daß kein Literal
garantieren, daß kein Literal 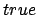 und
und 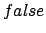 gleichzeitig ist.
gleichzeitig ist.
Nun erstellen wir noch die beiden Gewinne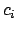 und
und 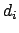 für jedes Literal
für jedes Literal 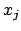 zum Auffüllen, welche an j-ter Stelle eine
zum Auffüllen, welche an j-ter Stelle eine 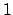 bzw. eine
bzw. eine 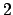 stehen haben:
stehen haben:
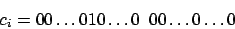
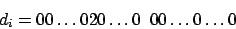
Aus den so entstandenen Gewinnen läßt sich nun genau der Rucksack voll ausschöpfen (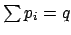 ), wenn die
), wenn die 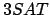 -Formel erfüllt ist.
-Formel erfüllt ist.
Beispiel
Gegeben sei folgende aussagelogische Formel:
Der SUBSUM-Gewinn für 4 Klauseln und 3 verschiedene Literale ist
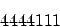
Wir erzeugen folgende Gewinne
Eine gültige Belegung mit der wir genau den richtigen Gewinn treffen ist also
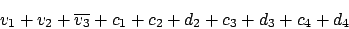
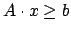 mit ganzzahligen Koeffizienten gegeben. Gefragt ist, ob es einen Lösungsvektor
mit ganzzahligen Koeffizienten gegeben. Gefragt ist, ob es einen Lösungsvektor 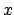 gibt, dessen Komponenten
gibt, dessen Komponenten 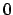 oder
oder 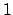 sind42, so daß die Gleichung
sind42, so daß die Gleichung
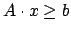 wahr ist.
wahr ist.
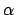 von
von 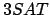 wieder der Form
wieder der Form
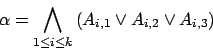
Die Matrix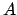 ist nun
ist nun 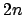 Zellen breit und
Zellen breit und 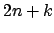 Zellen hoch, wobei
Zellen hoch, wobei 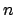 die Anzahl der unterschiedlichen Literale und
die Anzahl der unterschiedlichen Literale und 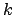 die Anzahl der Klauseln in
die Anzahl der Klauseln in 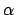 ist. Wir verwenden für das O/1-ILP in den einzelnen Zeilen der Matrix für ,,true'' eine
ist. Wir verwenden für das O/1-ILP in den einzelnen Zeilen der Matrix für ,,true'' eine 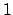 für ,,false'' eine
für ,,false'' eine 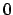 .
.
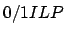 -Problem genau dann auch erfüllt ist, wenn die
-Problem genau dann auch erfüllt ist, wenn die 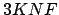 von
von 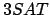 auch erfüllt ist.
auch erfüllt ist.
- SAT
 3SAT (lokale Ersetzung)
3SAT (lokale Ersetzung)
- 3SAT
 CP (Transformation)
CP (Transformation)
- 3SAT
 RP (Transformation sowie auch Spezialisierung)
RP (Transformation sowie auch Spezialisierung)
- 0/1 Integer Linear Programming (Transformation)
- Weitere NPC-Beweise
Einige NP-Vollständigkeitsbeweise
SAT  3SAT (lokale Ersetzung)
3SAT (lokale Ersetzung)
3SAT ist das Erfüllbarkeitsproblem mit der Voraussetzung, daß in der Formel Es ist klar, daß man für den NP-Vollständigkeitsbeweis genauso wie bei SAT die Guess-And-Check-Methode bei 3SAT anwenden kann.
Wir können SAT auf 3SAT polynomiell reduzieren:
1.Schritt
Mit Hilfe der De-Morgan-Regeln
und der Regel der doppelten Verneinung
erstellen wir einen Syntaxbaum aus der Eingabeformel
2.Schritt
Wir formen den so entstandenen Syntaxbaum um.
Dafür geben wir einem jeden Verknüpfungsknoten einen Namen, wobei
Nun kommt ein Äquivalenzoperator
Wir können auch folgendes Konstrukt erstellen:
Dies bedeutet, daß wenn der rechte und der linke Teil äquivalent sind, die Formel 1 ist, wenn beide Teile nicht äquivalent sind, dann ist der Wert der Formel 0. Wir können uns dies an einem Beispiel36 klar machen:
|
|
|||
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |

In den obigen Formel bemerken wir, daß wir höchstens immer 3 Literale pro Klausel in der Formel stehen haben37. Die Formeln
3SAT  CP (Transformation)
CP (Transformation)
3SAT Wir erzeugen den Graphen für das CP folgendermaßen:
- Für jede Klausel mit jeweils 3 Literalen erzeugen wir auch 3 Knoten.
- Wir zeichnen jeweils eine Kante zwischen allen Literalen zweier Klauseln. Einzige Ausnahme ist hierbei, daß die beiden Literale komplementär zueinander sind.
- Wir zeichnen niemals eine Kante zwischen den Literalen ein und derselben Klausel.
Beispiel
| 1.Klausel | ||||||
|
|
|
2.Klausel | ||||
|
|
3.Klausel |

3SAT  RP (Transformation sowie auch Spezialisierung)
RP (Transformation sowie auch Spezialisierung)
Gliedert sich in 2 Teile:
- SUBSUM
 RP (Spezialisierung)
RP (Spezialisierung)
- 3SAT
 SUBSUM (Transformation)
SUBSUM (Transformation)
Für die NP-Vollständigkeit von
Die Frage von
Gibt es eine Teilmenge aller Elemente mit dem Gewinn 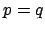 ?
?
Teil 2:
Es gilt zu beweisen39:
Sei die
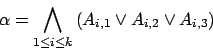
Die i-te Klausel hat folgende Form:
Wir setzen den zu erzielenden Gewinn gleich40

Wir erstellen für jedes Literal
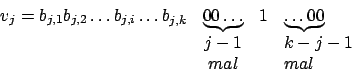
Dabei stellt
Dasselbe für
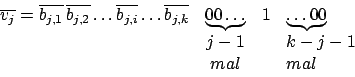
Nun erstellen wir noch die beiden Gewinne
Aus den so entstandenen Gewinnen läßt sich nun genau der Rucksack voll ausschöpfen (
Beispiel
Gegeben sei folgende aussagelogische Formel:
|
|
1.Klausel | |||||
|
|
2.Klausel | |||||
|
|
|
3.Klausel | ||||
|
|
4.Klausel |
Wir erzeugen folgende Gewinne
| Klauselnr. | 1234 | Im Rucksack | |
| 1100 | 001 | ||
|
|
0011 | 001 | |
| 1001 | 010 | ||
|
|
0110 | 010 | |
| 0101 | 100 | ||
|
|
1010 | 100 | |
| 1000 | 000 | ||
| 2000 | 000 | ||
| 0100 | 000 | ||
| 0200 | 000 | ||
| 0010 | 000 | ||
| 0020 | 000 | ||
| 0001 | 000 | ||
| 0002 | 000 |
0/1 Integer Linear Programming (Transformation)
Bei 0/1 Linear Programming ist ein lineares Gleichungssystem- 0/1 ILP ist in NP
Mittel Guess-and-Check-Verfahren läßt sich der Vektor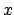 ermitteln und anschließend überprüfen.
ermitteln und anschließend überprüfen.
-
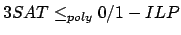
Wir reduzieren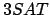 in polynomieller Zeit auf
in polynomieller Zeit auf 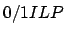 , d.h wir erzeugen für
, d.h wir erzeugen für 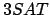 einen Algorithmus mit Hilfe von
einen Algorithmus mit Hilfe von 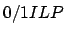 .
.
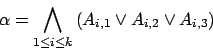
Die Matrix
- Die ersten
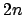 Ungleichungen stellen sicher, daß ein und dasselbe Literal nicht gleichzeitig wahr und falsch sein kann, bzw. auch eines der beiden sein muß und nicht gar nichts sein kann43:
Ungleichungen stellen sicher, daß ein und dasselbe Literal nicht gleichzeitig wahr und falsch sein kann, bzw. auch eines der beiden sein muß und nicht gar nichts sein kann43:
(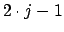 )te Formel:
)te Formel:
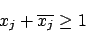
(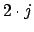 )te Formel:
)te Formel:
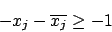
- Die letzten
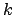 Ungleichungen sagen, daß pro Klausel ein Literal wahr sein muß:
Ungleichungen sagen, daß pro Klausel ein Literal wahr sein muß:
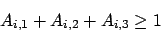
Weitere NPC-Beweise
Weitere NPC-Beweise findet man in der Fachliteratur.Fußnoten
- ... folgendermaßen35
- op ist ein Operator also entweder
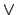 oder
oder 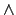
- ... Beispiel36
- Dies steht auf Seite 944 im Cormen: Introduction to Algorithms
- ... haben37
- Wenn wir weniger als drei haben, können wir ein weiteres Literal ergänzen, indem wir ein Literal der Klausel verdoppeln.
- ... reduzieren38
-
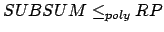
- ... beweisen39
- Wir erstellen einen Algorithmus für
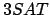 mit Hilfe von
mit Hilfe von 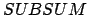 .
.
- ... gleich40
- Der zu erzielenden Gewinn für 3 Klauseln und 3 Literale wäre also 444111 (In Worten: vierhundertvierundvierzigtausendeinhundertundelf)
- ...
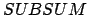 41
41 - Also, wenn wir 3 unterschiedliche Literale haben (
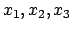 ), dann haben wir
), dann haben wir 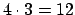 Gewinne
Gewinne
- ... sind42
- D.h. Maskierung der Zeilen in der Matrix mit dem Vektor x. Nur dort wo eine 1 vorkommt, wird auch die Spalte genommen.
- ... kann43
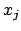 und
und
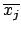 können, wie man an den Formeln sieht nicht gleichzeitig
können, wie man an den Formeln sieht nicht gleichzeitig 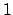 oder
oder  sein, sondern müssen paarweise verschieden sein.
sein, sondern müssen paarweise verschieden sein.