Unterabschnitte
![\includegraphics[scale=0.5]{mlp.eps}](img42.png)
Die Anzahl der Neuronen wird von der Inputschicht an hintereinander geschrieben. Obiges Netz ist z.B. ein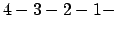 MLP.
MLP.
Man kann desweiteren hinter jede Nummer eine Zahl schreiben, die angibt, welche Kennlinie die Neuronen der jeweiligen Schicht haben. Für obiges Netz z.B.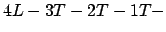 MLP.
MLP.
![\includegraphics[scale=0.75]{hinton.eps}](img57.png) Die einzelnen Kästchen variieren in Farbe und Größe. Große Kästen können z.B. hohe Beträge der Gewichte veranschaulichen. Schwarze Kästen negative Gewichte. Nicht ausgefüllte positive. Es sind auch Schattierungen der Kästen möglich.
Die einzelnen Kästchen variieren in Farbe und Größe. Große Kästen können z.B. hohe Beträge der Gewichte veranschaulichen. Schwarze Kästen negative Gewichte. Nicht ausgefüllte positive. Es sind auch Schattierungen der Kästen möglich.
Hintondiagramme eignen sich hervorragend um den Status eines neuronalen Netzes abzulesen. In Hintondiagrammen bilden sich bei einigen Lernaufgaben für neuronale Netze Muster. Weiterhin kann man gucken, wo eventuell Verbindungen gelöscht werden bzw. neu hinzugefügt werden.
- Aufbau
- Nomenklatur
- Hintondiagramm
- MLPs mit linearen Kennlinien lassen sich durch Matrixmultiplikation ausdrücken
Multilayer Perzeptron
Aufbau
![\includegraphics[scale=0.5]{mlp.eps}](img42.png)
- Die Neuronen der einzelnen Schichten sind bei MLPs vollverknüpft. Dabei gibt es nur Vorwärtsverknüpfungen (Feed forward net). Es werden keine Schichten übersprungen.
In der Literatur (z.B. Zell) findet man neuronale Netze von unten nach oben gezeichnet. Wir zeichnen hier von oben nach unten. - Die Indizes der Neuronen von links nach rechts der einzelnen Schichten laufen immer mit Kleinbuchstaben. Der größte Indize wird mit dem jeweiligen Großbuchstaben bezeichnet. Z.B. Inputschicht:
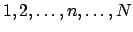
- Die Inputschicht wird mit
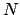 bezeichnet. Die Outputschicht mit
bezeichnet. Die Outputschicht mit 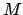 . Das Hiddenlayer mit
. Das Hiddenlayer mit 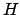 . Gibt es weitere Hiddenlayer, wie hier, werden diese mit Buchstaben nach
. Gibt es weitere Hiddenlayer, wie hier, werden diese mit Buchstaben nach 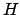 gekennzeichnet, also hier dritte Schicht von oben
gekennzeichnet, also hier dritte Schicht von oben 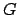 .
.
- Input und Output sind Vektoren. Diese werden manchmal durch einen
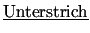 , manchmal durch einen
, manchmal durch einen
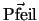 darüber, manchmal auch gar nicht gekennzeichnet.
darüber, manchmal auch gar nicht gekennzeichnet.
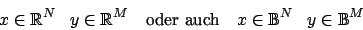
- Jede Schicht hat eine Gewichtsmatrix. Diese hat die Dimension
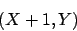
wobei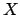 die Anzahl der Neuronen der darüberliegenden Schicht ist (also der Schicht von der die Schicht die Signale bekommt) und
die Anzahl der Neuronen der darüberliegenden Schicht ist (also der Schicht von der die Schicht die Signale bekommt) und 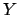 die Anzahl der Neurone der Schicht ist. Jedes Neuron der Schicht bekommt also eine Spalte der Matrix zugeteilt, in welche es seine Gewichte abspeichert.
die Anzahl der Neurone der Schicht ist. Jedes Neuron der Schicht bekommt also eine Spalte der Matrix zugeteilt, in welche es seine Gewichte abspeichert.
Hinweis: Wollen wir eine Schicht mit linearer Kennlinie mit Hilfe der Matrixmultiplikation berechnen, also die Gewichtsmatrix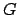 mit dem Vektor
mit dem Vektor 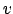 multiplizieren, so müssen wir die Matrix genau andersherum definieren: Eine Zeile ist nun für jedes Neuron reserviert. An forderster Stelle (also die gesamte erste Spalte der Matrix) steht der BIAS. Wir müssen den Vektor
multiplizieren, so müssen wir die Matrix genau andersherum definieren: Eine Zeile ist nun für jedes Neuron reserviert. An forderster Stelle (also die gesamte erste Spalte der Matrix) steht der BIAS. Wir müssen den Vektor 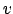 umschreiben, indem wir die erste Komponente
umschreiben, indem wir die erste Komponente  setzen und alle weiteren Komponenten nach unten verschieben. Führen wir die Matrixmultiplikation so durch, so erhalten wir als Ergebnis den Outputvektor der gesamten Schicht.
setzen und alle weiteren Komponenten nach unten verschieben. Führen wir die Matrixmultiplikation so durch, so erhalten wir als Ergebnis den Outputvektor der gesamten Schicht.
Nomenklatur
Obiges Netz stellt ein vierschichtiges oder dreistufiges Netz da. Bei ,,Stufennomenklatur'' wird die Eingabeschicht nicht als Stufe mitgezählt, weil diese sowieso nur die Eingaben weiterleitet.Die Anzahl der Neuronen wird von der Inputschicht an hintereinander geschrieben. Obiges Netz ist z.B. ein
Man kann desweiteren hinter jede Nummer eine Zahl schreiben, die angibt, welche Kennlinie die Neuronen der jeweiligen Schicht haben. Für obiges Netz z.B.
| T | Tangenshyperbolicus |
| L | Lineare Kennlinie |
| F | Fermi Funktion |
Hintondiagramm
![\includegraphics[scale=0.75]{hinton.eps}](img57.png)
Hintondiagramme eignen sich hervorragend um den Status eines neuronalen Netzes abzulesen. In Hintondiagrammen bilden sich bei einigen Lernaufgaben für neuronale Netze Muster. Weiterhin kann man gucken, wo eventuell Verbindungen gelöscht werden bzw. neu hinzugefügt werden.
MLPs mit linearen Kennlinien lassen sich durch Matrixmultiplikation ausdrücken
Den Output einer Schicht mit linearen Kennlinien kann man durch Vektor-Matrix-Multiplikation berechnen. Haben nun mehrere Schichten hintereinander lineare Kennlinien, so lassen sich all diese Schichten zu einer Schicht zusammenfassen, indem wir eine Matrixmultiplikation über die Gewichtsmatrixen durchführen.