Hilfssätze Determinanten
Für den Beweis beweisen wir zunächst folgende Hilfssätze:- Vertauscht man in der Matrix
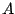 zwei Zeilen und erhält so die Matrix
zwei Zeilen und erhält so die Matrix 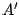 , so gilt
, so gilt
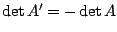 .
.
- Multipliziert man eine Zeile der Matrix
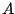 mit einem Skalar
mit einem Skalar 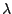 und erhält so
und erhält so 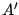 so gilt:
so gilt:
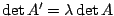 .
.
- Addiert man eine Zeile zu einer anderen Zeile in einer Matrix
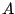 und erhält so die Matrix
und erhält so die Matrix 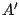 , so bleibt die Determinante davon unangetastet:
, so bleibt die Determinante davon unangetastet:
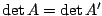 .
.