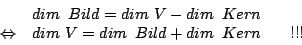Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Der Vektorraum » Dimensionssatz
Dimension Der Vektorraum Untervektorraum

Dimensionssatz

Sei $f:V\rightarrow W$ ($V,W$ sind $\mathbb{K}-$Vektorräume) eine lineare Abbildung. Dann gilt der Dimensionssatz:

\begin{displaymath}dim\,\,\, V= dim\,\,\, Bild(f)+dim \,\,\,Ker(f)\end{displaymath}

Beweis:
Bemerkungen:
$dim V:$ Die Anzahl der Vektoren der Basis von V.
$dim\,\,\, Bild(f):$ Die Anzahl der Vektoren im Untervektorraum Bild (f) von V
$dim\,\,\, Ker(f):$ Die Anzahl der Vektoren im Kern von f. Dies ist wiederum ein Untervektorraum von V.
  1. Da Ker (f) ein Untervektorraum von V ist ist auf jeden Fall

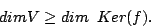
    \begin{displaymath}dim V\geq dim \,\,\,Ker(f).\end{displaymath}

    Die Vektoren der Basis des Kernes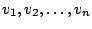 $v_{1},v_{2},\ldots,v_{n}$ sind linear unabhängig zueinander. Aufgrund des Basisergängzungssatzes kann man nun zu dieser Basis linear unabhängige Vektoren in 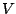$V$ hinzufügen und diese Basis so zu einer Basis von 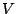$V$ ergänzen:

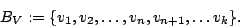
    \begin{displaymath}B_{V}:=\{v_{1},v_{2},\ldots,v_{n},v_{n+1},\ldots v_{k}\}.\end{displaymath}

  2. Wir lassen nun die Abbildung 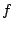$f$ auf der Basis des Vektorraums 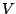$V$ laufen. So erhalten wir

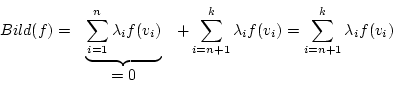
    \begin{displaymath} \begin {array}{lcl} Bild(f)=&\underbrace{\sum_{i=1}^{n}\lamb... ...tyle\sum_{i=n+1}^{k}\lambda_{i}f(v_{i})\\ &=0&\\ \end {array}\end{displaymath}

    Die Basisvektoren des Kerns werden auf die 0 abgebildet. Somit ist die Anzahl der Basisvektoren des Bildes und damit die Dimension des Bildes

    \begin{displaymath}\begin {array}{rll}&dim\,\,\,Bild=dim\,\,V-dim\,\,\,Kern&\\ ... ...&dim\,\,V=dim\,\,\,Bild+dim\,\,\,Kern&\,\,\,\,\,!!!\end {array}\end{displaymath}

$\Box$

Dimension Der Vektorraum Untervektorraum