Unterabschnitte
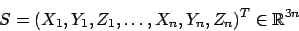
Im Texturvektor die Farbwerte der Punkte
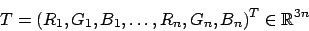
- Laserscans
- Bilden eines Vektors
- Linearkombination
- Bilden eines Durchschnittsgesichtes
- Verbesserung der Qualität
Was wurde gemacht (Blanz/Vetter)
Laserscans
Es wurde ein 3D-Laserscan an 100 Frauen und 100 Männern gemacht. Dabei entsteht sowohl eine Texture-Map des Gesichtes wie auch ein Bild mit Tiefeninformationen. Für den Scan wurden diverse Einschränkungen gemacht:- Haare mit Badekappe abgedeckt. Kein Makeup. Bart abrasiert.
- Alle Gesichter haben einen neutralen Gesichtsausdruck.
- Kopf am Hals abgeschnitten.
- Hinter den Ohren Schnitt gemacht.
- Aufnahmen wurden Normalisiert.
Bilden eines Vektors
Das Gesicht wird in einen Shape-Vektor und einen Texturvektor konvertiert. Im Shapevektor finden wir nacheinander die 3D Koordinaten der PunkteIm Texturvektor die Farbwerte der Punkte
Linearkombination
Wir können neue Gesichter mittels Linearkombination9 aus den alten Gesichtern des Vektorraums bilden. Zum Beispiel lassen sich Gesichter mit baryzentrischen Koordinaten10 ausdrücken. Mit dieser Methode ist nun das Korospondenzproblem zwischen zwei Gesichtern ein mathematisches Optimierungsproblem.
Bilden eines Durchschnittsgesichtes
Aus den erhaltenen Daten kann man ein allgemeines Durchschnittsgesicht erzeugen, welches die Mittelwerte darstellt.Verbesserung der Qualität
Man kann einzelne Gesichtsregionen abtrennen. Hier wird anatomisches Wissen benutzt, welches sagt, welche Gesichtsregionen voneinander unabhängig sind. Analog wäre dies eine Aufteilung des Vektorraums.Fußnoten
- ... Linearkombination9
- Damit das geht, braucht man natürlich genügend viele Gesichter. Des weiteren war auch vor diesem Experiment gar nicht klar, dass so etwas gehen könnte.
- ... Koordinaten10
- Hierbei wird ein Punkt in der Ebene als Linearkombination der Eckpunkte eines gleichschenkligen Dreiecks gesehen, dessen Rand insgeamt die Länge
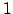 hat.
hat.