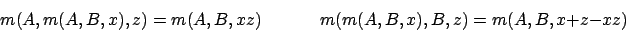Ψ Die Informatikseite

Menü
Informatik » Master » Computeranimation » Gesichtsanimation mit Morphing » Morphingfunktion
2D-Gesicht zu 3D-Gesicht (Blanz/Vetter) Gesichtsanimation mit Morphing Wahrscheinlichkeitsrechnung

Morphingfunktion

Sei $\Omega$ eine Menge von Objekten (also ein Vektorraum) zum Beispiel von Gesichtern. Die Morphingfunktion ist wie folgt definiert:

Sei $A,B\in\Omega$ und $x\in [0..1]$. Eine Abbildung $m:\Omega\times\Omega\times[0..1]\rightarrow\Omega$ wird als Morphingfunktion bezeichnet, wenn sie für alle $x\in [0..1]$ definiert ist und gilt

\begin{displaymath}m(A,B,0)=A\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m(B,A,1)=B\end{displaymath}

An einer Morphingfunktion können bestimmte Eigenschaften getestet werden. Diese wären z.B. Injektivität, Distributiv. Gemacht haben wir die Eigenschaften linear, symmetrisch, ,,rein'' und bijektiv:
  • Eine Morphingfunktion ist linear, wenn gilt:

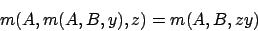
    \begin{displaymath}m(A,m(A,B,y),z)=m(A,B,zy)\end{displaymath}

  • Eine Morphingfunktion heißt symmetrisch, wenn gilt:

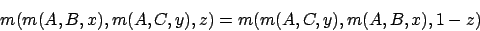
    \begin{displaymath}m(m(A,B,x),m(A,C,y),z)=m(m(A,C,y),m(A,B,x),1-z)\end{displaymath}

  • Eine Morphingfunktion heißt rein, wenn gilt:

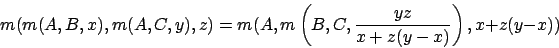
    \begin{displaymath}m(m(A,B,x),m(A,C,y),z)=m(A,m\left(B,C,\frac{yz}{x+z(y-x)}\right),x+z(y-x))\end{displaymath}

    Für den zweidimensionalen Fall gilt:

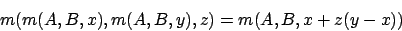
    \begin{displaymath}m(m(A,B,x),m(A,B,y),z)= m(A,B,x+z(y-x))\end{displaymath}

  • Eine Morphingfunktion ist bijektiv, wenn gilt

    \begin{displaymath}m(A,m(A,B,x),z)=m(A,B,xz)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m(m(A,B,x),B,z)=m(A,B,x+z-xz)\end{displaymath}


2D-Gesicht zu 3D-Gesicht (Blanz/Vetter) Gesichtsanimation mit Morphing Wahrscheinlichkeitsrechnung