Unterabschnitte
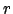 in eine parallele und in eine senkrechte Komponente zu
in eine parallele und in eine senkrechte Komponente zu 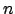 zerlegen:
zerlegen:
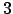 imaginäre Einheiten für die gilt:
imaginäre Einheiten für die gilt:
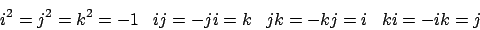
Auf Quaternionen kann eine Norm definiert werden
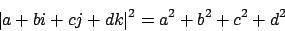
Einheitsquaternionen haben als Norm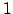 .
.
Das konjugierte Quaternion ist von der Form
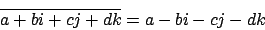
Für ein Einheitsquaternion gilt, dass das Inverse das konjugierte Quaternion ist
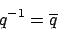
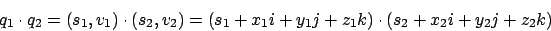
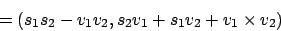
Mit Hilfe dieser Multiplikation können wir nun die Rotation eines Punktes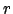 um eine Achse
um eine Achse 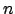 erzeugen. Wir setzen
erzeugen. Wir setzen
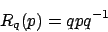
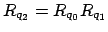 mit
mit
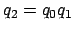 .
.
![$u\in [0,1]$](img92.png) anzugeben, über die linear interpoliert wird mit der Formel:
anzugeben, über die linear interpoliert wird mit der Formel:
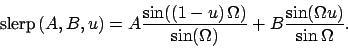
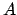 und
und 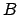 sind Einheitsquaternionen.
sind Einheitsquaternionen.
- Darstellung von Rotation mit Angular Displacement
- Quaternionen als Verallgemeinerung der komplexen Zahlen
- Rotation mit Quaternionen
- Sphärische lineare Interpolation
Quaternionen
Darstellung von Rotation mit Angular Displacement
Wir können eine Drehung mit Hilfe einer- Drehachse
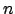 und
und
- einem Drehwinkel
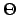
- Parallele Komponente:
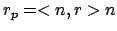
- Senkrechte Komponente:
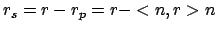
--
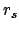 rotiert den Ortsvektor
rotiert den Ortsvektor 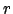 auf Position
auf Position 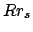 .
.
- Wir konstruieren einen Vektor
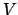 , der senkrecht zu
, der senkrecht zu 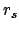 steht und senkrecht zu
steht und senkrecht zu 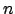 steht, also in der Ebene liegt6:
steht, also in der Ebene liegt6:
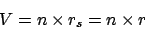
- Berechne
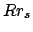 gemäß
gemäß
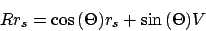
- Also
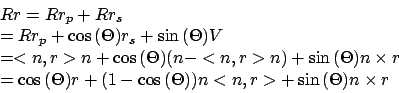
Quaternionen als Verallgemeinerung der komplexen Zahlen
Quaternionen sind 4-Tupel reeller Zahlen, auf denen eine Multiplikation definiert ist. Sie besitzen dementsprechendAuf Quaternionen kann eine Norm definiert werden
Einheitsquaternionen haben als Norm
Das konjugierte Quaternion ist von der Form
Für ein Einheitsquaternion gilt, dass das Inverse das konjugierte Quaternion ist
Rotation mit Quaternionen
Zwei Quaternionen lassen sich wie folgt multiplizierenMit Hilfe dieser Multiplikation können wir nun die Rotation eines Punktes
- Dabei ist
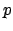 das rein imaginäre Quaternion, welches den zu rotierenden Punkt
das rein imaginäre Quaternion, welches den zu rotierenden Punkt 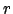 darstellt. Die Koordindaten des Punktes
darstellt. Die Koordindaten des Punktes 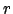 werden in den Imaginärteil des Quaternions abgebildet
werden in den Imaginärteil des Quaternions abgebildet
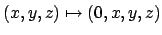 .
.
- Bilde
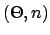 auf das Einheitsquaternion
auf das Einheitsquaternion
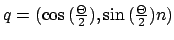 , wobei
, wobei 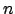 normiert sein muss7.
normiert sein muss7.
- Die Operation
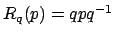 ergibt wieder ein rein imaginäres Quaternion, welches rotiert ist.
ergibt wieder ein rein imaginäres Quaternion, welches rotiert ist.
Sphärische lineare Interpolation
Leider interpoliert die normale Quaternionenrotation nicht linear. Man kann sich jedoch mit der sphärischen linearen Interpolation implementiert in SLERP Abhilfe verschaffen. Es ist eine LaufvariableFußnoten
- ... liegt6
- Das Kreuzprodukt erzeugt einen Vektor, der zu der Ebene, die durch beide Vektoren aufgespannt wird, senkrecht steht.
- ... muss7
- Man kann sehr einfach beweisen, dass wenn
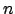 normiert vorliegt, dieses Quaternion ein Einheitsquaternion ist.
normiert vorliegt, dieses Quaternion ein Einheitsquaternion ist.