Unterabschnitte
Den Worst Case können wir abwenden, indem wir ein Element aus den möglichen wählbaren per Zufall auswählen. Hierbei kommen wir auf die Laufzeit
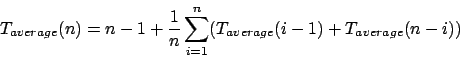
was wieder auf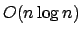 hinaus läuft.
hinaus läuft.
Das Monte Carlo Verfahren läuft in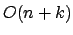 , wenn man voraussetzt, daß das Rechnen mit den Zahlen nur konstante Kosten verursacht.
, wenn man voraussetzt, daß das Rechnen mit den Zahlen nur konstante Kosten verursacht.
Zu dem Las Vegas Verfahren haben wir auch eine Laufzeitabschätzung gemacht, in der wir gezeigt haben, mit welcher Wahrscheinlichkeit im Monte Carlo Verfahren ein Fehler auftritt und mit welcher Laufzeit wir dann den Fehler ausbügeln.
Eine Hashmenge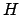 heißt universell, wenn es in ihr mindestens soviele unterschiedliche Hashfunktionen gibt, wie es Schlüssel im Schlüsseluniversum gibt.
heißt universell, wenn es in ihr mindestens soviele unterschiedliche Hashfunktionen gibt, wie es Schlüssel im Schlüsseluniversum gibt.
- Las Vegas & Monte Carlo
- Randomisiertes Quicksort
- Mustererkennung - Karp&Rabin
- Universelles Hashing
- Skip-Listen
Randomisierte Algorithmen
Randomisierte Algorithmen können für die selbe Eingabe unterschiedliche Laufzeit und unterschiedlichen Speicherplatz benötigen.Las Vegas & Monte Carlo
| Las Vegas | Monte Carlo |
| für ,,nein'' immer korrekt | für ,,nein'' immer korrekt |
| für ,,ja'' immer korrekt | für ,,ja'' manchmal4falsch |
| immer korrekt | für ,,ja'' manchmal falsch |
Randomisiertes Quicksort
Wir hatten gesehen, daß Quicksort im Worst Case eine sehr schlechte Laufzeit hat, da das Pivotelement falsch gewählt wird. Haben wir zum Beispiel eine schon vorsortierte Folge und wollen diese noch einmal mit Quicksort sortieren und nehmen dabei immer das erste Element, so haben wir den Worst Case.Den Worst Case können wir abwenden, indem wir ein Element aus den möglichen wählbaren per Zufall auswählen. Hierbei kommen wir auf die Laufzeit
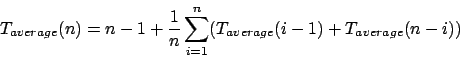
was wieder auf
Mustererkennung - Karp&Rabin
Wir benutzen eine Fingerprinttechnik. Wir teilen das Muster durch eine Primzahl. Ebenso teilen wir auch den Text von der Länge des Musters fortlaufend immer durch eine Primzahl. Sobald bei den beiden Divsionen derselbe Rest herauskommt, ist die Wahrscheinlichkeit hoch, daß das Muster mit dem Text an dieser Stelle übereinstimmt. Dieses Verfahren ist aber ein Monte Carlo Verfahren. Es kann bei der Antwort ,,ja'' auch sein, daß das Muster nicht gleich dem Text ist, wenn die beiden Zahlen ungünstig liegen. Um dieses Verfahren in ein Las Vegas verfahren umzuformen, müssen wir, wenn das Monte Carlo Verfahren ein ,,ja'' zurückgibt dieses mit einem naiven Vergleichen noch überprüfen.Das Monte Carlo Verfahren läuft in
Zu dem Las Vegas Verfahren haben wir auch eine Laufzeitabschätzung gemacht, in der wir gezeigt haben, mit welcher Wahrscheinlichkeit im Monte Carlo Verfahren ein Fehler auftritt und mit welcher Laufzeit wir dann den Fehler ausbügeln.
Universelles Hashing
Beim Hashing kann es vorkommen, daß alle Werte im Worst-Case auf einen Wert abgebildet werden. Um dieses zu umgehen verwenden wir beim universellen Hashing eine Hashmenge, aus der wir zufällig eine passende Hashfunktion auswählen, die dann das Hashing optimal macht, so daß wir keine oder nur wenige Kollisionen haben.Eine Hashmenge
Skip-Listen
- Skiplisten sind normale Listen, denen ,,Überholspuren'' aufgesetzt sind, um Listenglieder zu überspringen und so eine schnellere Suche zu fördern. Die ,,Höhe'' eines Listenelementes ist damit definiert, wie viele Skiplisten über diesem Listenelement einen Stopp haben.
- Die perfekte Skipliste ermöglicht es sogar, in der Zeit
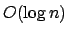 zu suchen.
zu suchen.
- Randomisierte Skiplisten sind Skiplisten für die die Höhe der einzelnen Listenglieder zufällig festgelegt wird.
- Einfüge und Löschoperationen auf Skiplisten sind sehr aufwendig, weil die Liste rekonstruiert werden muß, weshalb nur weniger solcher Operationen auf solchen Listen durchgeführt werden sollten.
Fußnoten
- ... manchmal4
- aber seltenst