Unterabschnitte
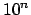 Schritte von Nöten sind:
Schritte von Nöten sind:
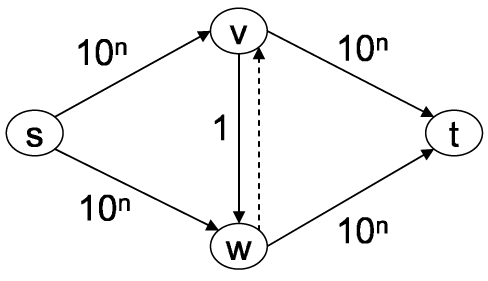 Zuerst wird die Kante von (s,v) genommen und dann über die 1-er-Kante (v,w) gegangen, um über (w,t) dann ins Ziel zu gehen. Im nächsten Schritt wird über (s,w) gegangen, dann über die Rückwärtskante (w,v) und dann über (v,t) zum Ziel. Durch ungeschickte Wahl der Kanten wird das Verfahren sehr ineffinzient, obwohl es schneller gehen könnte.
Zuerst wird die Kante von (s,v) genommen und dann über die 1-er-Kante (v,w) gegangen, um über (w,t) dann ins Ziel zu gehen. Im nächsten Schritt wird über (s,w) gegangen, dann über die Rückwärtskante (w,v) und dann über (v,t) zum Ziel. Durch ungeschickte Wahl der Kanten wird das Verfahren sehr ineffinzient, obwohl es schneller gehen könnte.
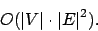
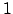 beschrifteten Kante liegen darf. Ein Beispiel für ein bipartites Matchingproblem ist zum Beispiel die Computerzuteilung für verschiedene Aufgaben. Nicht alle Aufgaben lassen sich auf allen Computern lösen. Von einem Aufgabenknoten ziehen wir eine Kante mit der Kapazität 1 zu einem Computer, der diese Aufgabe erfüllen könnte. Dieses Matchingproblem lösen wir, indem wir vor alle Aufgabenknoten einen Startknoten setzen und diesen mit einer 1-er-Kante mit allen Aufgabenknoten verbinden und von jedem Computerknoten auch wieder eine 1-er-Kante zu einem neu hinzugefügten Zielknoten hinzufügen. Das ganze kann man so als ein Netzwerkflußproblem betrachten.
beschrifteten Kante liegen darf. Ein Beispiel für ein bipartites Matchingproblem ist zum Beispiel die Computerzuteilung für verschiedene Aufgaben. Nicht alle Aufgaben lassen sich auf allen Computern lösen. Von einem Aufgabenknoten ziehen wir eine Kante mit der Kapazität 1 zu einem Computer, der diese Aufgabe erfüllen könnte. Dieses Matchingproblem lösen wir, indem wir vor alle Aufgabenknoten einen Startknoten setzen und diesen mit einer 1-er-Kante mit allen Aufgabenknoten verbinden und von jedem Computerknoten auch wieder eine 1-er-Kante zu einem neu hinzugefügten Zielknoten hinzufügen. Das ganze kann man so als ein Netzwerkflußproblem betrachten.
Netzwerkflußproblem
Das Netzwerkflußproblem ist das Problem des maximalen Flusses von einem Startknoten zu einem Zielknoten. Hierbei können durch die Kanten Flüsse fließen, wobei die Inschrift einer jeden Kante angibt, wie hoch der Fluss in dieser Kante momentan ist und maximal sein darf.- Bei einem Knoten, der kein Start oder Zielknoten ist, gehen genausoviele Flüsse weg, wie reinkommen. Die Summe aller einkommenden Flüsse minus die Summe aller herausgehenden Flüsse ist also 0.
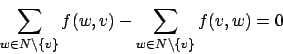
- Wir können das Flußdiagramm über die Kanten an jeder Stelle in zwei Stücke schneiden. Sei
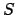 die Menge der Knoten die auf der einen Seite dieses Schnittes liegen. Der Nettofluß ist definiert mit
die Menge der Knoten die auf der einen Seite dieses Schnittes liegen. Der Nettofluß ist definiert mit
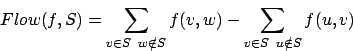
- Für alle Schnitte gilt: Der Nettofluß ist für jeden Schnitt gleich.
- Die Kapazität ist der maximal Fluß, der über einen Schnitt geführt werden kann. Es gilt

- Es gilt: Der maximale Fluß über das gesamte Netzwerk ist die minimalste Kapazität, die durch einen Schnitt gehen kann:
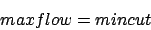
Ford&Fulkerson-Algorithmus
Algorithmus
- Wir schreiben an jede Kante ein Wertepaar
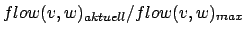 . Zudem erzeugen wir für jede Kante eine Rückwärtskante, die zu Beginn mit
. Zudem erzeugen wir für jede Kante eine Rückwärtskante, die zu Beginn mit 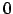 initialisiert wird.
initialisiert wird.
- Wir suchen immer wieder einen zunehmenden Pfad in dem Netzwerk. Dies kann dadurch geschehen, daß wir eine Erreichbarkeitsanalyse (z.B. mit der Breitensuche gestartet mit dem Startknoten) auf dem Restgraphen durchführen, welches in der Laufzeit
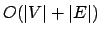 geschehen kann.
geschehen kann.
- Wir erhöhen entlang des zunehmenden Pfades alle aktuellen Flußwerte um den gefundenen Flußwert des Pfades.
- Dies tun wir solange, bis kein zunehmender Pfad mehr gefunden werden kann. (d.h. der Schnitt mit dem geringsten Fluß (mincut) ist voll ausgelastet.)
Worst Case
Der Worst-Case ist gegeben, wenn eine Kante immer wieder vor und dann die Rückwärtskante wieder zurück gegangen werden muß. Folgendes Beispiel ist ein Worst Case bei dem