Unterabschnitte
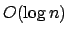 . Schlechteste AVL-Bäume sind Fibonaccibäume. Bei diesen steht die Fibonaccizahl
. Schlechteste AVL-Bäume sind Fibonaccibäume. Bei diesen steht die Fibonaccizahl 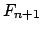 in der Wurzel.
in der Wurzel.
Wenn ein B-Baum die Ordnung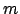 hat, dann bedeutet das, daß jeder Knoten mindestens
hat, dann bedeutet das, daß jeder Knoten mindestens 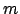 aber höchstens
aber höchstens 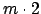 Schlüsselwerte mit den dazugehörigen Daten beinhaltet. (Davon ist die Wurzel ausgenommen)
Schlüsselwerte mit den dazugehörigen Daten beinhaltet. (Davon ist die Wurzel ausgenommen)
B-Bäume haben folgende Eigenschaften:
Beim Löschen kann es passieren, daß ein Knoten zu klein wird (UNDERFLOW). Wenn es möglich ist, borgen wir uns Schlüsselwerte von einem benachbarten Bruderknoten. Hierbei geht ein Wert aus dem Bruder in den gemeinsamen Vaterknoten, während ein Schlüsselwert aus dem Vaterknoten in den Knoten mit dem UNDERFLOW kommt. Geht dies nicht, so wenden wir Konkatenation an und zwei Bruderknoten werden zu einem Knoten zusammengefügt. Dieser Knoten nimmt des weiteren noch den Wert aus dem Vaterknoten auf, der nun auf keinen Sohn mehr zeigt.
Die Laufzeit von Suchen, Einfügen und Löschen auf B-Bäumen ist
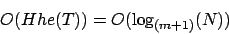
wobei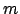 die Ordnung und
die Ordnung und 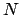 die Schlüsselanzahl.
die Schlüsselanzahl.
- Hashing
- Verschiedene Hashfunktionen
- Offenes Hashing mit Kollisionslisten
- Geschlossenes Hashing mit offener Adressierung
- Dynamisches Hashing
- Balancierte Bäume
Speichermöglichkeiten von Datenmengen mit dynamischer Größe
Hashing
Beim Hashing wird mit Hilfe einer surjektiven Funktion das Universum auf einen kleineren Speicher abgebildet.Verschiedene Hashfunktionen
- Modulofunktion:
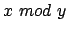 wobei
wobei 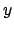 die Größe des Hashspeichers ist
die Größe des Hashspeichers ist
- Mittelquadrat: Die Speicheradresse wird quadriert. Danach werden aus der quadrierten Zahl in der Mitte Ziffern herausgenommen: Beispiel:
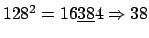
- Multiplikationsmethode: Die Zahl wird mit einer irrationalen Zahl zwischen
![$]0,1[$](img106.png) multipliziert. Danach erhalten wir eine Orignial+d-bittige Zahl. Die letzten d Bits werden als Speicheradresse für den Hash verwendet.
multipliziert. Danach erhalten wir eine Orignial+d-bittige Zahl. Die letzten d Bits werden als Speicheradresse für den Hash verwendet.
Offenes Hashing mit Kollisionslisten
Wenn es Kollisionen gibt, dann werden an den Hashspeicher Listen angehängt, in denen Elemente gespeichert werden, die nicht mehr in den normalen Speicher passten, weil diese schon besetzt war.Geschlossenes Hashing mit offener Adressierung
Beim geschlossenen Hashing mit offener Adressierung wird bei belegten Hashspeicherplätzen mittels anderer Hashfunktionen auf andere Speicherplätze ausgewichen.Dynamisches Hashing
Schon einmal berechnete Ergebnisse von Teilproblemen eines großen Problems werden gespeichert. Diese können aber problemlos gelöscht werden, wenn ein neuer Wert die Hashspeicherzelle überschreibt, da sie neu berechnet werden können.Balancierte Bäume
Bei den Bäumen ist jeweils das Verhalten beim Einfügen und Entfernen wichtig.Höhe von Bäumen
| leerer Teilbaum: | -1 |
| ein Knoten: | 0 |
| usw. |
Suchbäume
Bei einem INORDER-Durchlauf eines Suchbaumes sind alle Elemente sortiert.AVL
- Wenn
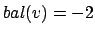 und
und
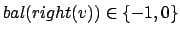 einfache Rotation nach links
einfache Rotation nach links
- Wenn
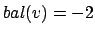 und
und
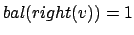 Doppelrotation rechts-links
Doppelrotation rechts-links
- Wenn
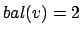 und
und
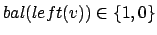 einfache Rotation nach rechts
einfache Rotation nach rechts
- Wenn
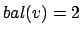 und
und
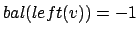 Doppelrotation links-recht
Doppelrotation links-recht
Blatt
In den inneren Knoten werden nur die Schlüssel, die zur Suche benötigt werden, gespeichert. Die eigentlichen Informationen stehen in den Blättern. Dabei sind die Blätter zum besseren sequentiellen Auslesen untereinander doppelt verknüpft.B-Bäume
B-Bäume sind Speicherstrukturen für den externen Speicher.Wenn ein B-Baum die Ordnung
B-Bäume haben folgende Eigenschaften:
- Jeder Knoten, außer die Wurzel hat mindestens
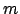 und höchstens
und höchstens 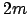 Schlüsselwerte, wobei
Schlüsselwerte, wobei 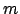 die Ordnung ist.
die Ordnung ist.
- Die Wurzel hat höchstens
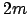 Schlüsselwerte. Nach unten gibt es jedoch keine Grenze.
Schlüsselwerte. Nach unten gibt es jedoch keine Grenze.
- Jeder Knoten mit
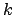 Schlüsselwerten hat
Schlüsselwerten hat 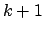 Söhne, wenn dieser Knoten nicht ein Blatt ist.
Söhne, wenn dieser Knoten nicht ein Blatt ist.
- Alle Blätter haben dieselbe Tiefe bezüglich des Wurzelknotens.
Beim Löschen kann es passieren, daß ein Knoten zu klein wird (UNDERFLOW). Wenn es möglich ist, borgen wir uns Schlüsselwerte von einem benachbarten Bruderknoten. Hierbei geht ein Wert aus dem Bruder in den gemeinsamen Vaterknoten, während ein Schlüsselwert aus dem Vaterknoten in den Knoten mit dem UNDERFLOW kommt. Geht dies nicht, so wenden wir Konkatenation an und zwei Bruderknoten werden zu einem Knoten zusammengefügt. Dieser Knoten nimmt des weiteren noch den Wert aus dem Vaterknoten auf, der nun auf keinen Sohn mehr zeigt.
Die Laufzeit von Suchen, Einfügen und Löschen auf B-Bäumen ist
wobei